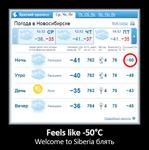
Seijon
Eugeny Homkin
9 users currently subscribed to this user.
After signing in, you can subscribe this user.
Итальянский информационный дизайнер Джоржия Лупи нарисовала уникальную инфографику, посвященную всем победителям Нобелевской премии с 1901 по 2012 год.
www.brainpickings.org …
%Инфографика
www.brainpickings.org …
%Инфографика
www.fontanka.ru …
Мигранты с 1 декабря будут обязаны подтверждать свои знания русского языка...Согласно закону, иностранные граждане, которые планируют трудиться в жилищно-коммунальном хозяйстве, розничной торговле или сфере бытового обслуживания, обязаны подтверждать владение русским языком не ниже базового уровня. При этом подтверждать знание языка нужно как при получении, так и при продлении разрешения на работу в России.
... <b>Граждане стран, где русский язык — государственный, подтверждать его знание не должны.</b> Зря, по-моему.
Мигранты с 1 декабря будут обязаны подтверждать свои знания русского языка...Согласно закону, иностранные граждане, которые планируют трудиться в жилищно-коммунальном хозяйстве, розничной торговле или сфере бытового обслуживания, обязаны подтверждать владение русским языком не ниже базового уровня. При этом подтверждать знание языка нужно как при получении, так и при продлении разрешения на работу в России.
... <b>Граждане стран, где русский язык — государственный, подтверждать его знание не должны.</b> Зря, по-моему.
Да ладно вам. Там все просто. примерно так как тут на 2:10 я думаю: www.youtube.com …
Ссылки на время не отрабатывают в местном проигрывателе почемуто.
Ссылки на время не отрабатывают в местном проигрывателе почемуто.
// и не только вы двое...
и как реакция? пугаются? :-)
Мне это напоминает теорему Геделя [о неполноте] ru.wikipedia.org …
Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.
Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой арифметики.
Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.
Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой арифметики.